История быстрого преобразования Фурье (БПФ) уходит в прошлое и связана с работами сделанных в разное время и разными людьми. Сама идея была предложена Жаном Батистом Джозефом Фурье в начале 19 века. Идея алгоритма быстрого вычисления основана на работах Джеймса Кули и Джона Уайлдера Тьюки. В 1965 году они разработали метод, который существенно уменьшил количество операций, необходимых для выполнения расчётов.
В настоящее время, благодаря современным модификациям и оптимизации этот метод стал неотъемлемой частью современной вычислительной техники. Он применяется в обработке сигналов и изображений, в криптографии, телекоммуникациях, а также многих других областях науки и техники.
Время чтения: 15 минут
Любой массив данных может быть преобразован (интерполирован) в непрерывный сигнал, при этом также любой непрерывный поток информации может быть разделён на дискретные части (дискретизирован). При работе большими массами информации возникает необходимость в выявлении в них каких-либо зависимостей и закономерностей, а также определении частотных компонентов. Так, например:
- при обработке аудио, видео, а также других сигналов, – это выявление их спектральных характеристик;
- в области цифровой обработки изображений – это улучшение качества и плотности сжатия;
- в медицинской диагностике – изучение биомедицинских импульсов;
- в финансовой аналитике – изучение временных колебаний цен на акции, а также другой финансовой информации.
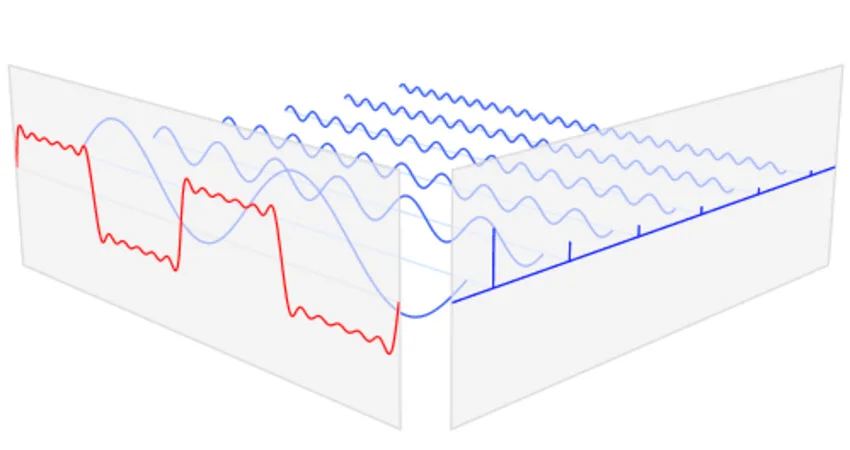
Что такое БПФ? Для чего используется?
Преобразование Фурье – это математический метод, применяемый для анализа сигналов. Он даёт возможность преобразовать данные из временной области в частотную, разлагая их на составляющие.
Быстрое преобразование Фурье (Fast Fourier transform – FFT) — это более эффективный алгоритм, применяемый для вычисления дискретных сигналов или последовательности данных. Он существенно сокращает количество операций, необходимых для выполнения вычислений, что значительно ускоряет весь процесс расчётов.
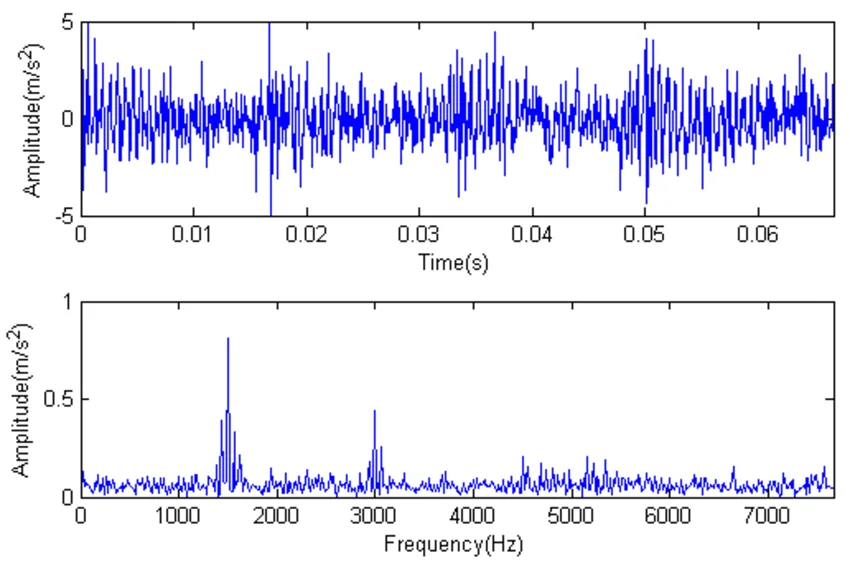
Если сравнивать эти методы преобразования, то мы можем наблюдать существенные различия в вычислительной скорости. Так, классический способ имеет квадратичную сложность – О(N^2) (здесь N — количество элементов во входной последовательности), а БПФ обладает линейно-логарифмической сложностью – О(N*log(N)).
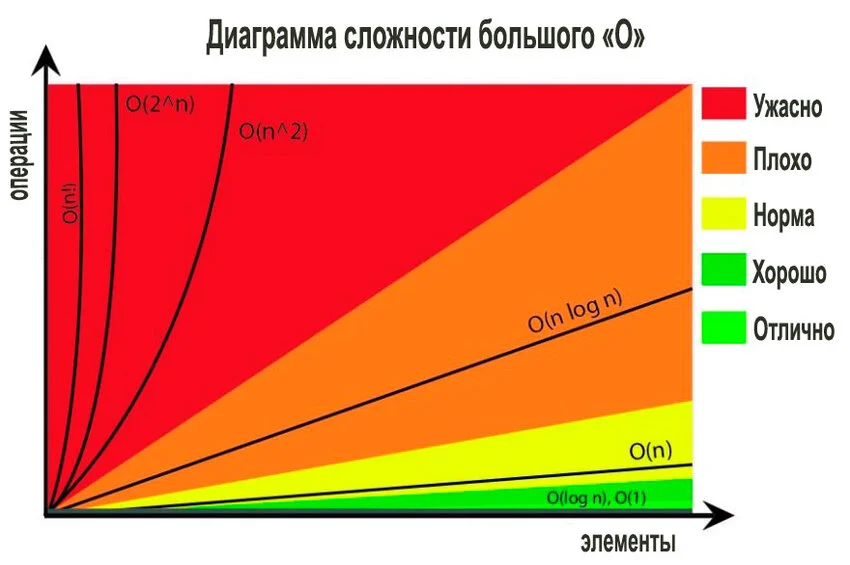
O(1) — постоянная;
O(n) — линейная;
O(n log n) — линейно-логарифмическая;
O(n^2) — квадратичная;
O(2^n) — экспоненциальная;
O(n!) — факториальная.
Сравнивая линейно-логарифмическую и квадратичную сложность, можно увидеть, как объём исходной информации влияет на количество необходимых вычислительных операций.
| Число элементов (N) | Число операций | |
| О(n*log(n)) | О(n^2) | |
| 10 | 34 | 100 |
| 100 | 665 | 10 000 |
| 1000 | ~ 10 000 | 1 млн. |
| 10 000 | ~ 133 000 | 100 млн. |
| 1 000000 | ~ 20 млн. | 1 000 млрд. |
Поэтому использование вычислений, имеющих линейно-логарифмическую сложность, существенно ускоряет процесс, особенно при работе с большими объёмами информации.
Для каких целей используют быстрое преобразование Фурье?
Этот тип анализа находит широкое применение в различных областях благодаря своей эффективности и скорости. Вот некоторые из основных целей, для которых он используется:
- Цифровая обработка.
- Обработка изображений.
- Телекоммуникационная связь.
Исследование частотных характеристик аудиосигналов помогает выделять звуковые особенности, отделять доминирующие частоты, фильтровать шумы и проводить компрессию файлов, сохраняя при этом качество звучания. В обработке видео FFT применяется для оценки каждого кадра, что даёт возможность удалить ненужные частоты, сжать видеоданные без существенных потерь в качестве, а также применять различные эффекты, такие как фильтрация и улучшение контрастности изображения.
Изображение, представляющее собой пиксельное пространство, переводится в частотный ряд. Представление картинки в виде набора частот используется в целях их обработки и фильтрации. Оно позволяет применять различные фильтры, осуществлять устранение шумов, улучшать контраст, выделять границы и отдельные детали.
Такая операция может быть обращена в пространство пикселей. Эта возможность значительно упрощает процесс обработки изображений и позволяет выполнять сложные операции с данными, с высокой эффективностью.
Всё это находит применение в областях компьютерного зрения, а также в компрессии и улучшении качества картинки.
Разбивка сигналов на составляющие по частоте, существенно упрощает их исследование и обработку при модуляции и демодуляции. Так, в системах множественного доступа, где исходная несущая разбивается на несколько поднесущих, каждая из них анализируется отдельно для более эффективной передачи.
Также FFT применяется для сжатия передаваемой информации, и устранения помех в каналах связи. Изучение спектрограммы даёт возможность убрать часть данных, несущих меньшую важность, что снижает размер передаваемых файлов без существенных потерь в качестве. Например, выделение помех и шумов в каналах связи, помогает фильтровать нежелательные составляющие, что повышает качество передачи. инки.
- Компрессия.
При сжатии данных можно предварительно проанализировать исходную последовательность в частотной области, что даёт возможность удалить лишние или менее важные составляющие, несущие меньше информации, без существенных потерь. Спектральные исследования применяется при сжатии аудиоформатов типа MP3, а также в методах компрессии изображений, в таких форматах, как JPEG.
В целом всё это существенно сокращает размер файлов, ускоряя их передачу, а также уменьшая размер места, необходимого под хранение, при этом сохраняется приемлемое качество.
.png "Изначальный аудиоспектр")
- Медицинская диагностика.
- Финансовая аналитика.
В медицинской диагностике, а именно в электроэнцефалографии (ЭЭГ) и электрокардиографии (ЭКГ), БПФ используется для изучения частотных характеристик электросигналов, генерируемых мозгом или сердцем. Это позволяет выявлять различные аномалии в активности мозга или сердечном ритме, особенности отдельных компонентных составляющих, а также помогает в диагностике различных состояний и заболеваний.
Также этот метод анализа используется в обработке данных с медицинских сканеров (например, МРТ и КТ). Его применение позволяет проанализировать снимок, выделить отдельные структуры, определить интересующие области, отфильтровать шумы, и в целом улучшить качество картинки для более точной диагностики заболеваний.
Здесь находит своё применение дискретное преобразование Фурье (ДПФ) в финансовой аналитике при изучении временных рядов финансовых данных, таких как ценные бумаги, валюты или стоимость активов. Оно даёт возможность проводить частотный анализ, выделяя циклические или периодические паттерны. Финансовые аналитики используют этот анализ для выявления скрытых циклов в рыночных трендах или сезонности в изменениях цен, что помогает прогнозировать возможные тенденции и поведение рынка.
Кроме этого, его используют для фильтрации и удаления шумов из финансовых временных рядов, что даёт возможность аналитикам выделять особенности и тренды, скрывающиеся за случайными колебаниями цен. В целом такой анализ помогает улучшить предсказательные модели для принятия более обоснованных финансовых решений.
- Криптография.
В криптографических системах может использоваться исследование спектральных характеристик шифруемых файлов. Например, при .создании или взломе криптографических методов, FFT может помочь в исследовании случайности или особенностей шифруемых сообщений, а также в обнаружении возможных уязвимостей в шифрах, связанных с частотными особенностями.
Также, в криптографии его используют для реализации различных методов шифрования и дешифрования, таких как алгоритмы RSA или шифрование спектра. Некоторые алгоритмы криптографии используют FFT для предварительного изменения сообщений перед шифрованием и дешифрованием, что улучшает безопасность данных и усложняет попытки расшифровки.
Свойства преобразования Фурье
Свойства FFT описывают ключевые характеристики этого метода расчётов для дискретно представленных данных, они включают в себя: линейность, независимость, растяжение, симметрию и сохранение энергии. Эти свойства являются ключевыми при их использовании в обработке информации, а также некоторых других задачах, где требуется переход между временной и частотной областями.
Линейность
Свойство линейности означает, что если взять сумму двух функций и выполнить их преобразование, то результат будет равен сумме их индивидуальных преобразований. Это также верно при их умножении на константу. Линейность является ключевой особенностью при исследовании, поскольку позволяет эффективно манипулировать данными при применении FFT.
Независимость от сдвига
Независимость от сдвига означает, что смещение по временной шкале не влияет на частотную шкалу спектра, а только на фазовую составляющую. Когда происходит смещение по времени, то спектр также сдвигается по частоте на ту же величину, однако это не меняет саму форму спектра, а лишь вносит фазовый сдвиг в каждую компоненту. Эта особенность позволяет анализировать характеристики независимо от их положения во времени
Растяжение по частоте
Свойство растяжения указывает на то, что изменение частоты, например, аудиосигнала по шкале времени приводит к растяжению или сжатию его спектрограммы. Если частота увеличивается, то спектр будет сильнее растянут вдоль оси частот. Также верно и обратное явление. При уменьшении частоты во времени ведёт к сжатию результирующей спектрограммы. Это свойство позволяет понимать, как изменения во времени влияют на спектральные характеристики.
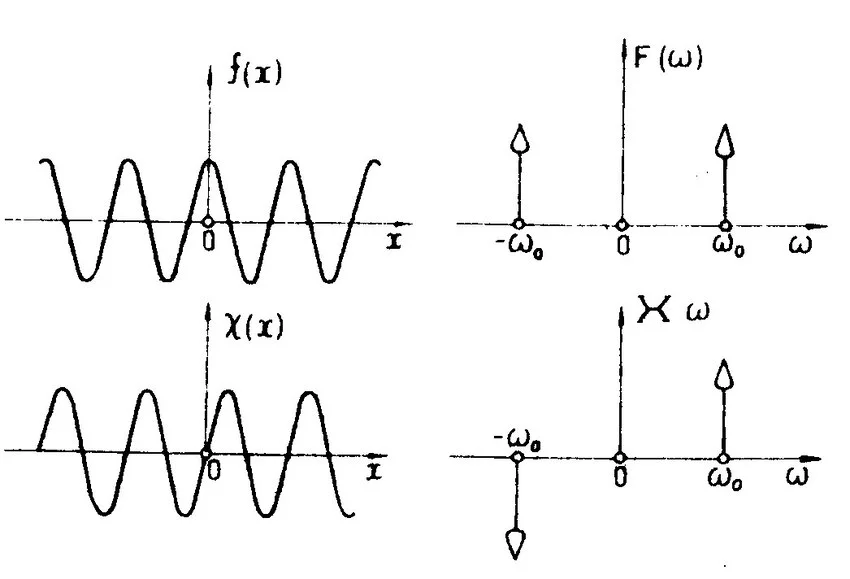
Симметрия
Симметрия относится к свойству, при котором спектральные характеристики функции в частотной области связаны с её временными характеристиками. Для вещественных функций симметрия проявляется следующим образом: если функция является чётной (симметричной относительно оси ординат), то её спектр будет действительным и чётным. Если она нечётна (симметрична относительно начала координат), то её спектр будет мнимым и нечётным. Это свойство позволяет анализировать характеристики сигналов, опираясь на их особенности во временной области и наоборот.
Сохранение энергии
Свойство сохранения энергии указывает на то, что энергия входной волны остаётся постоянной как во временной, так и в частотной области. Это означает, что сумма квадратов амплитуд во временной области равна сумме квадратов амплитуд в частотной. Такое сохранение энергии позволяет анализировать и обрабатывать информацию в различных областях, сохраняя их общую энергию при переходе от одной формы представления к другой.
В чём заключается фундаментальный принцип БПФ?
Обработка аналогового сигнала методом БПФ состоит из нескольких этапов. Первоочередными из них выступают дискретизация и оцифровка.
Дискретизация – это процесс перевода непрерывной функции в дискретный формат, путём измерения её значений в определённые моменты времени. Этот шаг позволяет представить непрерывную функцию в виде последовательности дискретных значений, что облегчает её дальнейший анализ на цифровых устройствах.
Оцифровка – это процесс, при котором данные после дискретизации преобразуются в цифровой формат путём кодирования их значений в числовую последовательность. Это даёт возможность компьютерам и иным цифровым устройствам обрабатывать, а также хранить информацию в цифровой форме.
Последующие этапы входят в сам процесс БПФ:
- Разделение на чётные и нечётные компоненты
- Выполнение рекурсии.
- Комбинирование результатов.
- Обратное перемешивание результатов.
Сначала последовательность данных разделяется на чётные и нечётные элементы. Это создаёт две подпоследовательности, где элементы на чётных позициях образуют одну подпоследовательность, а элементы на нечётных позициях - другую.
Для каждой из полученных подпоследовательностей выполняется рекурсивное вычисление. Этот этап продолжается, до тех пока длина последовательности не станут достаточно маленькой для прямого вычисления без дальнейшего разделения.
После рекурсивных расчётов для чётных и нечётных подпоследовательностей выполняется их комбинирование для получения итогового результата всей исходной последовательности.
В случае необходимости выполнения обратного преобразования Фурье, перехода от спектрограммы к дискретному состоянию, результаты объединяются, а затем выполняется их обратное перемешивание, для получения исходной последовательности.
Основываясь на описанных этапах, можно заключить, что фундаментальный принцип Быстрого преобразования Фурье заключается в разделении задачи на более мелкие подзадачи, применении к этим подзадачам БПФ, а также последующего комбинирования результатов для получения итогового полного преобразования. Такая методика даёт возможность значительно сократить количество необходимых операций, существенно уменьшая длительность расчётов.
Интерпретация результатов
Результаты быстрого преобразования Фурье представляют собой частотный спектр входной дискретной последовательности данных. Интерпретация этих результатов зависит от конкретной задачи и контекста, в котором используется FFT. Вот несколько общих способов интерпретации результатов:
- Оценка частотных компонент:
- Фильтрация и отбор:
- Сравнение с базовыми шаблонами:
- Определение характеристик:
Амплитудно-частотный график даёт возможность увидеть, какие частоты преобладают в исходном сигнале. При этом высокие пики амплитуды на графике указывают на преобладающие частоты.
После вычислений можно проанализировать спектрограмму в целях фильтрации или отбора определённых частотных компонентов. Например, убрать шумы или выделить интересующие частоты.
Сравнение спектрограммы с известными шаблонами спектров может использоваться для определения сходства или различий между различными сигналами.
Анализ ширины пиков, их амплитуды, а также распределения помогает в определении различных характеристик, таких как частоты основных компонентов, их силу и даже взаимосвязь между ними.
