Цифровая обработка сигналов (ЦОС) связана с важными вкладами нескольких учёных, совершённых в первой половине 20 века. Так, в 1933 году советский инженер и математик Владимир Котельников опубликовал работу, в которой впервые сформулировал концепцию о возможности восстановления непрерывной функции из конечного числа её выборок и определил их минимум.
При этом пятью годами ранее Гарри Найквист сформулировал критерии, которые также подчеркнули важность частоты дискретизации (ЧД) для точного восстановления информации.
И уже в 1949 году американский математик, криптоаналитик и инженер Клод Элвуд Шеннон своей работой «Mathematical Theory of Communication» внёс существенный вклад в теорию ЦОС, а также сформулировал математические принципы, которые связали труды Котельникова и Найквиста.
В результате совместных усилий этих учёных была сформулирована теория, которая и сегодня служит основой для аналого-цифрового преобразования во многих сферах.
Время чтения: 14 минут
Разработка теоремы стала основой для бурного развития аудио- и видеосистем, телекоммуникаций и ряда других областей, где ЦОС – неотъемлемая часть технологии.
Перед тем как перейти к сущности теоремы и описать, каков практический смысл в дискретизации аналоговых сигналов, рассмотрим понятия аналоговой и цифровой информации, ЧД, спектра и другие.
Аналоговая информация
Аналоговый сигнал (АС) представляет собой тип передачи данных, где они представлены в непрерывной форме. В контексте электроники и электротехники он заключается в изменении напряжения или тока во времени. В других процессах описывается непрерывной функцией, не обязательно периодической.
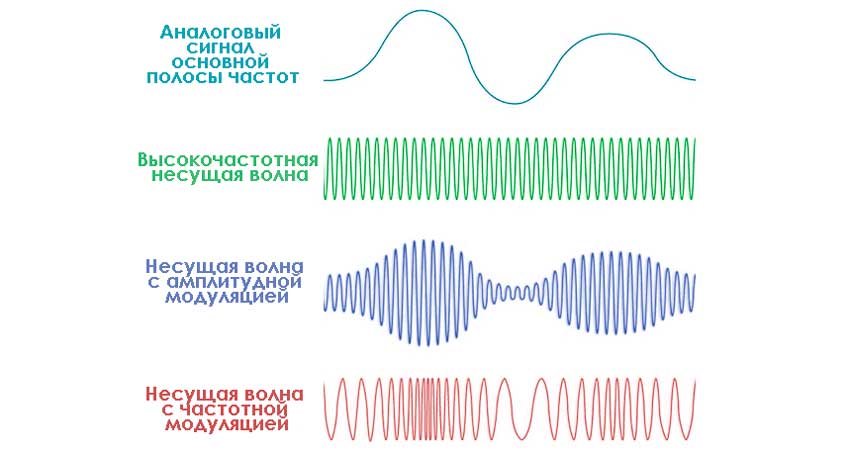
Примеры аналоговой системы широко распространены в природе:
- Скорость ветра в любой местности непостоянна. На неё влияют многие факторы: смена дня и ночи, времён года, прохождение циклонов и антициклонов. Интенсивность способна меняться как плавно, так и резко (порывы ветра).
- Такая же ситуация с температурой и давлением атмосферного воздуха. На них влияют те же факторы: суточные годовые изменения освещённости, явления в атмосфере.
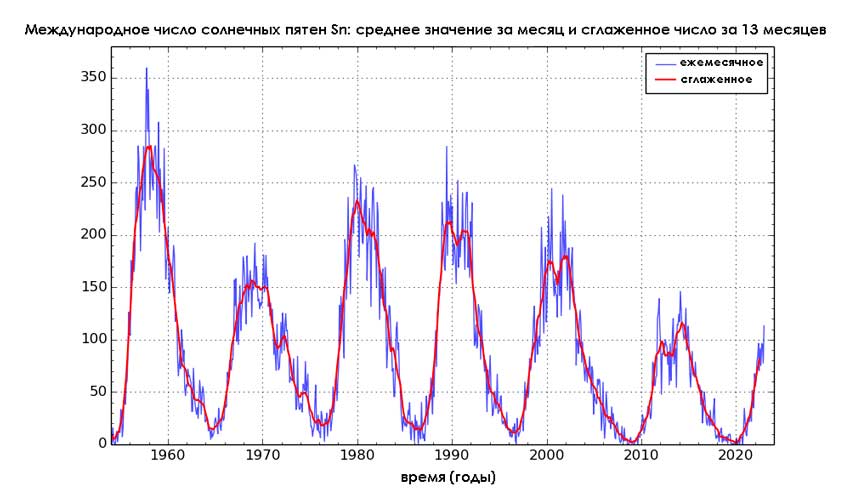
- Даже солнце не постоянно. Изменение светимости, интенсивности солнечного ветра напрямую зависят от протекающих внутри звезды термоядерных реакций, продолжающихся миллионы лет.
- В растительном мире также встречаются непрерывно протекающие процессы. Рост растений, например, деревьев, не прерывается до момента их гибели. При этом существует неравномерность развития: суточную или годовую.
- Также хороший пример – течение воды в реках и движение волн в море. Все эти явления непрерывны и изменчивы во времени.
Цифровая информация
В отличие от АС, которые представляют непрерывные изменения показателей, в цифровых сигналах (ЦС) информация заключена в виде дискретных значений, как правило, последовательности нулей и единиц. Большинство ЦС создаются из АС посредством их преобразования, однако есть примеры, когда дискретные данные генерируется в чистом виде:
- При игре на музыкальных инструментах, не только электронных, каждое действие музыканта является дискретным. Например, нажатие на клавишу синтезатора или удар полочкой по барабану. Дискретной единицей здесь выступает нота.
- Широко распространённым источником ЦС являются электронные часы. Они отображают дату и время в целых числах.
- Ещё одним дискретным источником принято считать текстовое и числовое отображение. Оно представляется буквами и цифрами на листе бумаги или экране компьютера.
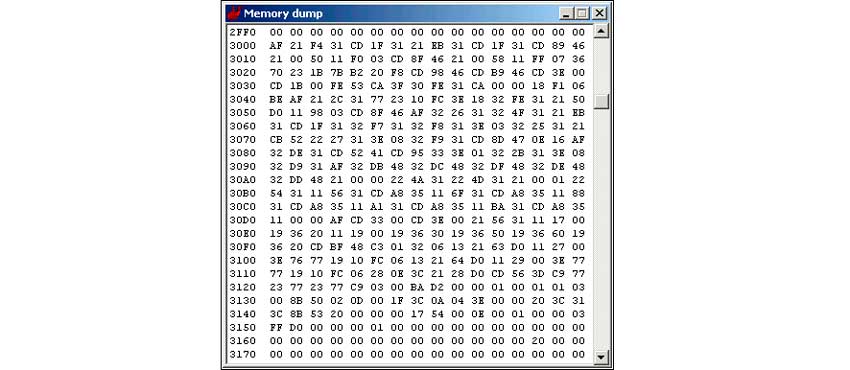
- Также сведения, находящиеся в файлах, объединённых в блоки, представлены бинарным, шестнадцатеричным или символьным кодом.
- QR-коды, штрихкоды и бар коды также встречаются повсеместно: на продуктах питания, бирках товаров и даже исторических зданиях. Определённая последовательность точек или штрихов на них – дискретные данные.
- Другим примером могут служить единицы измерений, например, длинна, угол и иные. Во всех измерительных инструментах шкалы дискретны. Это позволяет с необходимой точностью определить измеряемый параметр.
Ключевая идея заключается в том, что в АС представлен непрерывным потоком данных, в отличие от дискретных, разделённых порциями, как в ЦС.
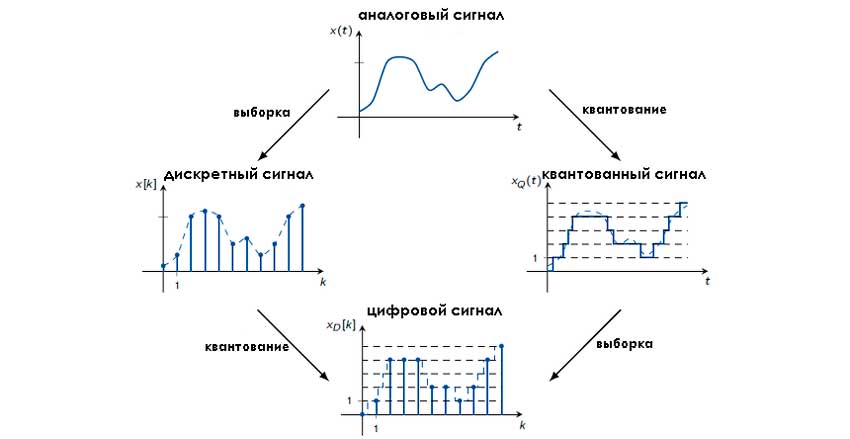
Оцифровка
Благодаря повсеместной цифровизации, появилась большая необходимость в преобразовании аналогового сигнала в цифровой код. Помимо дискретизации, еще применяют квантование. Этот метод встречается в ПЗС (CCD) матрицах фотокамер. Отличие заключается в том, что при дискретизации регистрируют мгновенные значения амплитуды через равные промежутки времени. При квантовании же фиксируют усреднённое значение регистрируемого параметра в определённом временном отрезке. Здесь важную роль играет разрядность квантования.
Необходимость дискретизации
Основными причинами, требующими деление информации на «порции» это:
- Хранение и передача данных. АС более чувствительны к шумам и потерям в процессе дата-трансфера по сравнению с цифровыми. Дискретизация позволяет сохранять данные в «цифре», что делает их более устойчивыми к помехам, а также обеспечивает эффективную передачу по каналам связи.
- Обработка и анализ. Многие методы, такие как фильтрация, компрессия, усиление и анализ, легче выполнять с цифровыми данными. То же относится и к применению цифровых алгоритмов для улучшения качества, извлечения, анализа.
- Интеграция с цифровыми устройствами. Многие приборы: компьютеры, камеры, передающая аппаратура, работают в цифровом формате. Это позволяет интегрировать АС в цифровые системы для обработки, хранения и дальнейшего использования информации.
Частота дискретизации
Это важный параметр АЦП, который определяет, как часто мы берём образцы АС для его преобразования. Фактически это количество измерений или отсчётов, сделанных в течение определённого промежутка времени.
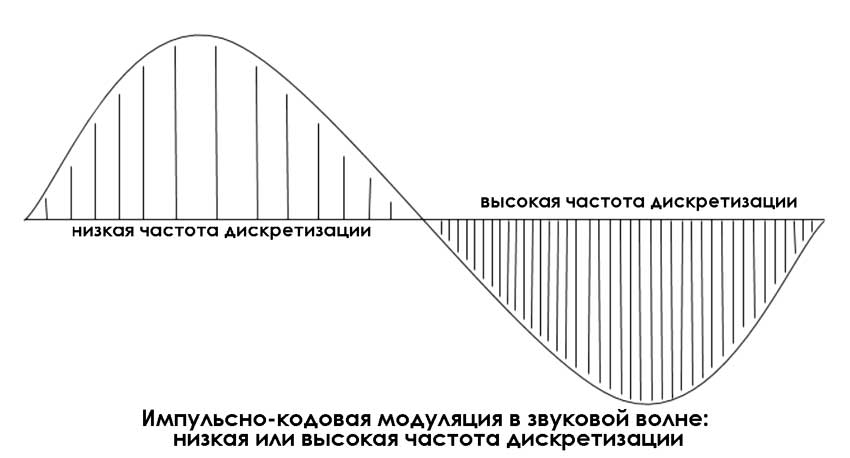
В аналого-цифровом преобразовании, термин теорема Найквиста, в чистом виде не используется и не упоминается в литературе. Работы Котельникова и Шеннона привели к слиянию общих наработок в области АЦП и появлению единой концепции. Её называют теоремой Котельникова в российской, а Шеннона – Найквиста — в англоязычной литературе.
Частота Найквиста – это важный показатель в АЦП. Он отражает, какова должна быть минимальная периодичность выполнения выборок, чтобы АС получилось эффективно восстановить. Фактически число Найквиста – это минимально необходимая частота дискретизации аналого-цифрового преобразователя.
Спектр
Простейшим аналоговым сигналом является синусоидальная волна. Она имеет свою амплитуду, длину и периодичность повторения.
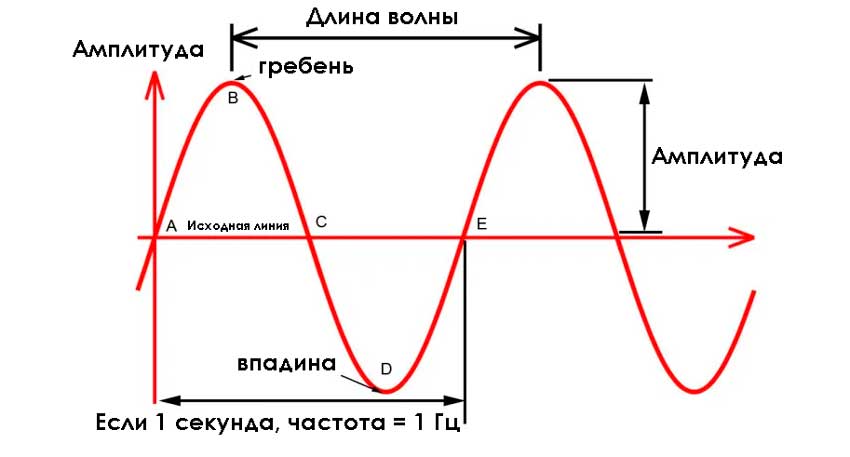
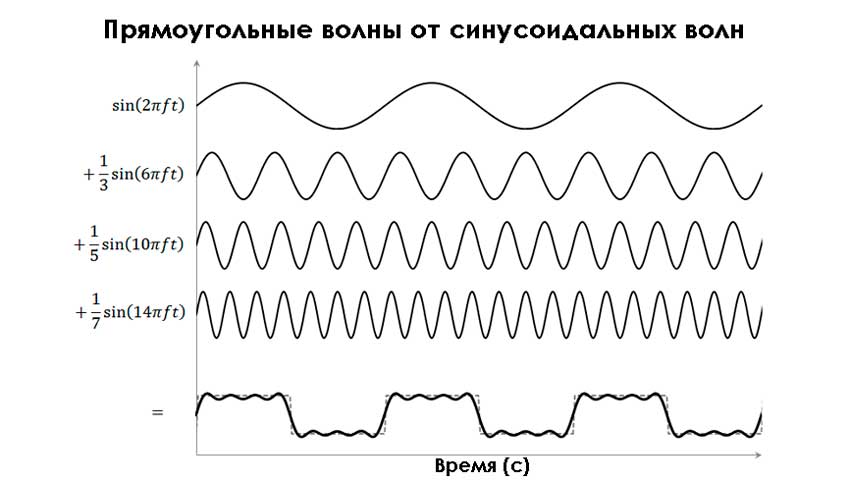
Однако в большинстве своём АС имеет сложную форму и его невозможно описать какой-либо простой функцией. Для этого используют преобразование Фурье. Оно позволяет разложить её в виде алгебраической суммы простых функций. Каждая вносит свой вклад и имеет собственную амплитуду и частоту. Так что спектр сигнала – это график, на котором отражены частоты преобразовываемого АС. Спектр описывается амплитудно-частотной характеристикой.
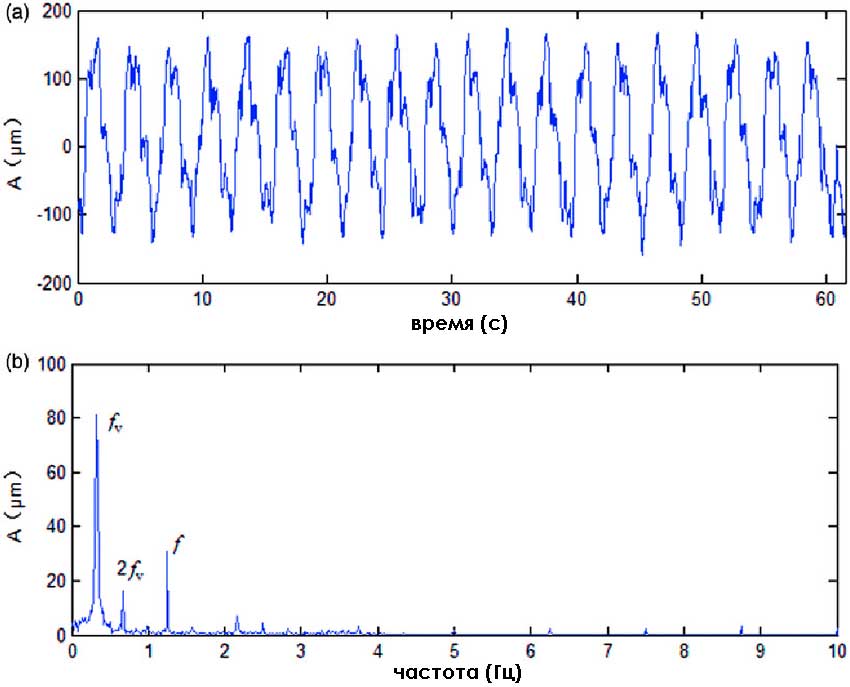
Теорема Котельникова
Её определение следующее: непрерывный сигнал s(t), который ограничен по спектру частотой fв, определяется совокупностью мгновенных значений (отсчётов) s(tк) в моменты времени tк = k . ∆t, отстоящие друг от друга на временной интервал.
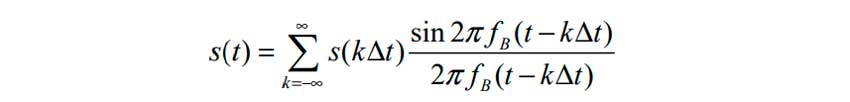
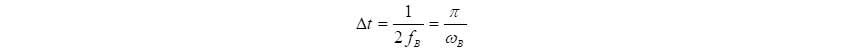
То есть это означает, что периодичность, с которой мы должны измерять наш АС, зависит от параметров той его составляющей, что имеет максимальную частоту. При этом выборка осуществляется с периодичностью не меньше чем в два раза, превышающей частоту fв.
Ограничение выборки
Чтобы понять причину, почему выборка ограничена, рассмотрим пример. Если для синусоидальной волны с интенсивностью колебаний в 5 герц сделать её с разной периодичностью, то увидим, что при малом периоде собранные данные не будут достоверно отражать истинную форму исходной волны.
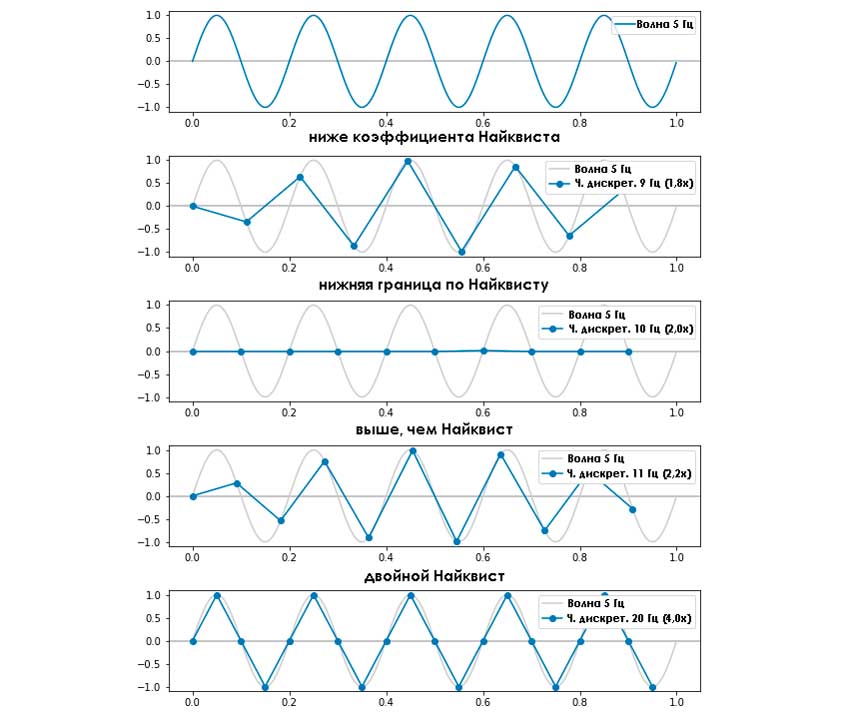
Однако так как большинство АС не описываются простыми функциями, то рассмотренный нами пример с синусоидой является исключением, так как для него недостаточно двукратного превышения частоты. При такой форме волны требуется четырёхкратное превышение ЧД. Однако в большинстве случаев при АЦП достаточно использовать частоту Найквиста.
Иные ограничения
Применение этой теоремы сопряжено с определёнными ограничениями, а именно:
- Ограничение частотной ширины спектра. Если он распределён по бесконечному диапазону, то теорема не применима.
- Применения аналоговых фильтров. Для правильной оцифровки необходимы фильтры, которые предназначены для устранения высокочастотных составляющих, выходящих за пределы частотного диапазона.
- Ограничение по времени. Теорема предполагает, что дискретизация непрерывных сигналов невозможна, поэтому они обязаны иметь конечный период.
- Наличие смещения. Например, если имеется постоянная амплитуда, то это нередко приводит к потере информации или искажениям при дискретизации.
- Ограничения обработки и хранения данных. Дискретизация с большой частотой требует большего объёма памяти для хранения данных и вычислительных мощностей. Поэтому такое ограничение называют физическим или техническим.
Эти ограничения не означают, что теорема неприменима вообще, а лишь указывают на условия, при которых она доступна к применению без утери информации, снижения передаточной характеристики и иных существенных искажений.
Области применения
Практическое применение теоремы встречается во всех областях, в которых задействована цифровая техника. Рассмотрим некоторые из них.
Цифровая обработка.
Здесь её применение помогает избежать потери данных и появления артефактов при обработке высокочастотной информации как на этапе аналого-цифрового, так и цифро-аналогового преобразования.
Телекоммуникация.
В области телекоммуникаций применяется для определения минимальной пропускной способности канала связи. Это устраняет риск появления эффекта алиасинга и иных искажений передаваемой информации.
Обработка видео и изображений.
В этой области она позволяет определить максимальную ЧД и пропускную способность канала, при которой изображение или видео правильно восстанавливаются и передаются без потерь.
Аналоговая электроника.
В аналоговой электронике расчёты используются для определения ширины полосы пропускания фильтров. Это помогает избежать искажений при обработке данных.
Также теорема применяется в сотовой связи, электронной навигации, радиоастрономии, аудио- и видеотехнике, и электронике.
Советы по использованию
Для правильной оцифровки нужно, чтобы ЧД быть не меньше, чем удвоенная максимальная частота в исходном АС. Таким образом, её выбор является первоначальным шагом.
- Вначале определяется максимальная частотная составляющая. Это выполняется путём анализа амплитудного спектра или визуализации его формы с помощью специального программного обеспечения.
- После этого выберите ЧД, вдвое превышающую максимальную, обнаруженную при анализе спектрограммы. Например, если она составляет 10 кГц, то дискретизации осуществляется не менее чем на 20 кГц.
- Поскольку аналого-цифровое преобразование иногда сопровождается алиасингом (наложением частот или общим искажением), потребуется применить фильтрацию. Это делается с использованием фильтров низкой частоты перед выборкой или постобработки после неё.
- Так как существует вероятность потери информации из-за выбора недостаточно высокой выборки, то стоит убедиться, что выбранная ЧД позволяет сохранить достаточное её количество, необходимое для адекватной его обработки и восстановления.
- Если при первоначальном выборе ЧД возникнут проблемы с сохранностью данных, то её уточняют, увеличивая значение. Однако важно помнить, что это также потребует более высоких вычислительных ресурсов и повышает сложность обработки.
При всей простоте теоремы Котельникова нужно помнить, что её применимость имеет ряд ограничений и допущений. Благодаря ей мы достигаем баланса между эффективным использованием ресурсов при хранении и трансфере данных, а также сохранить достаточно информации, которая помогает точно восстановить аналоговые сигналы.
