
Когда разные люди слышат слово «ключ», то первые мысли и образы, пришедшие в головы, разнятся: им открывают замок, ещё это — источник воды и даже знак на нотном стане. Слово одно, а понятий несколько. Филологи подобное явление называют омонимом.
А что приходит в вашу светлую голову, когда слышите слово «фильтр»? Устройство для очистки водопроводной воды? Способ приготовления кофе? Цепочка из резистора и конденсатора? Если последнее, то поздравляю: вы определённо имеете отношение к электронике. Если нет, не огорчайтесь: материал написан для постигающих азы этой сферы. Она рассказывает о базовом узле практически любого более-менее сложного электронного устройства.
Из статьи вы узнаете о фильтрах в электронике, познакомитесь с их функциональными разновидностями, типами и различными схемотехническими решениями без погружения в математические дебри. Для лёгкости понимания и демонстрации работы будут приведены ссылки на интерактивные модели, которые читатель самостоятельно опробует.
![]() Время чтения: 20 минут
Время чтения: 20 минут
Фильтры в электронике? Это очень просто!
Фильтры любой разновидности или схемотехнического решения необходимы для работы большинства электронных схем. В интересах каждого, кто занимается проектированием электрооборудования или электроприборов, уметь разрабатывать их схемы, способные соответствовать заданному набору спецификаций. К сожалению, многие, особенно вступающие в бескрайние дали электроники, смутно представляют предмет: либо из-за отсутствия знакомства с ним, либо из-за нежелания разбираться в математике, связанной с проектированием сложных элементов.
Эта статья станет простым введением в определённые фундаментальные концепции и термины. Она не превратит новичка в проектировщика, но послужит отправной точкой для желающих узнать больше о проектировании.
Общие сведения о фильтрации и фильтрах
В теории электроцепей так называют электрическую цепь (смотри статью «ТОП-10 узлов в схемотехнике аналоговых устройств») ,меняющую амплитудные и/или фазовые характеристики сигнала в зависимости от его частоты.
Идеальный компонент не изменяет частотность у имеющихся составляющих входного сигнала (ВС) и не добавляет новые частотные уровни, а меняет только их амплитуды и/или фазы. Фильтры часто используются в схемотехнике для выделения определённого требуемого частотного диапазона с одновременным подавлением других. Скажем, устройство демонстрирует определённое усиление, зависящее от частоты ВС.
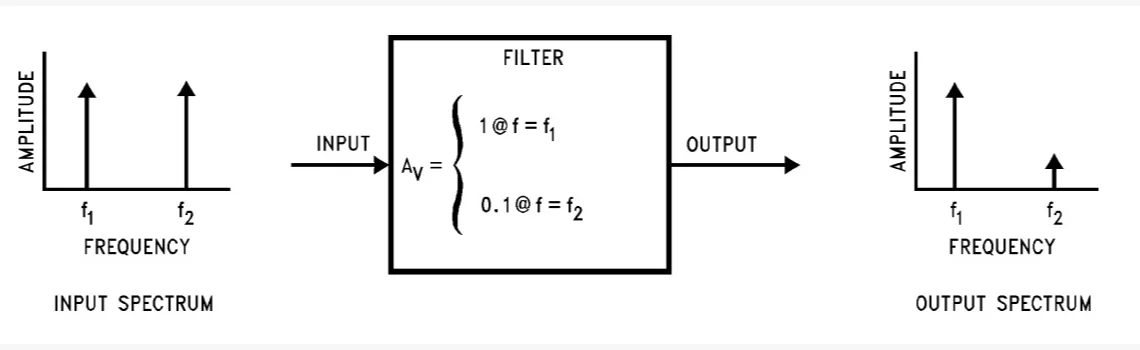
В качестве примера рассмотрим ситуацию, когда к полезному ВС f1 нежелательным образом подмешивает второй с частотным показателем f2. Если суммарный сигнал пропустить через цепь с крайне низким усилением на f2 по сравнению с f1, то «ненужный» будет подавлен, а полезный останется, как и прежде. Нас не интересует усиление на любой другой частотности, кроме f1 и f2: пока вторая достаточно сильно подавлена относительно первой, фильтрация будет удовлетворительной.
Однако усиление указывается на нескольких различных частотах или в полосе, поскольку фильтры определяются их эффективностью в частотной области, а не на конкретном значении.
Их поведение как системы описывается математически и образует передаточную функцию (ПФ). Это отношение преобразований Лапласа его выходного-входного сигналов. Таким образом, ПФ напряжения H(s) в виде формулы выглядит так:
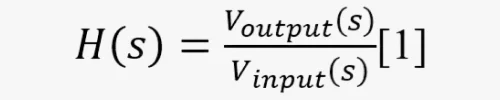
где Vinput и Voutput — входное и выходное напряжение сигнала, s — комплексный оператор ПФ в преобразовании Лапласа.
ПФ определяет поведение фильтра при любом, то есть произвольном ВС (аналоговый или дискретный, прямоугольный и пр.), но чаще интересует именно непрерывный синусоидальный. Особенно важна её характеристика как функция от частоты, определяющая влияние на амплитуды синусоидальных сигналов на различных значениях колебаний.
Знание ПФ (усиления) позволяет нам определить, насколько хорошо компонент различает разночастотные сигналы. Усиление в зависимости от частоты называется амплитудной, или когда речь идёт об обработке звука, амплитудно-частотной характеристикой (АЧХ).
Иногда приходится характеризовать ПФ как частотную, отражающую влияние на сдвиг фазы разночастотных синусоидальных сигналов. Такая характеристика называется фазовой или фазочастотной (ФЧХ). Поскольку изменение фазы также меняет сигнал во времени, она становится главнейшей при работе со сложными сигналами, где временно́е соотношение составляющих на разных частотах имеет решающее значение.
Заменив комплексный оператор в формуле [1] на jω, где j=√(-1), а ω — угловая частота (УЧ) 2πf, определим влияние фильтра на амплитуду[2] и фазу[3] ВС. Они находятся путём взятия абсолютного значения [1]:
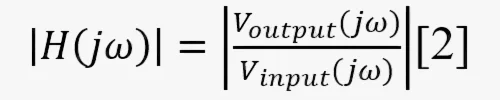
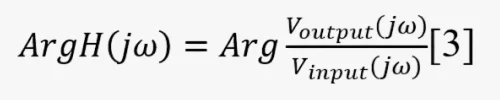
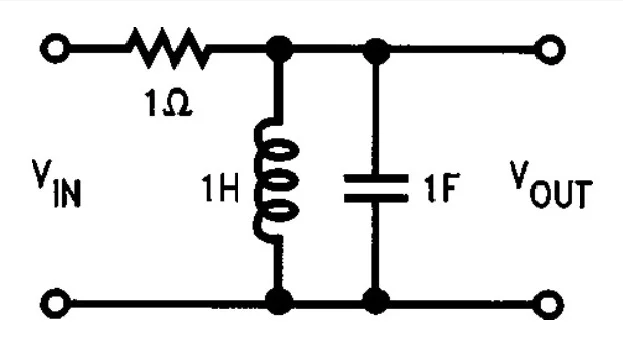
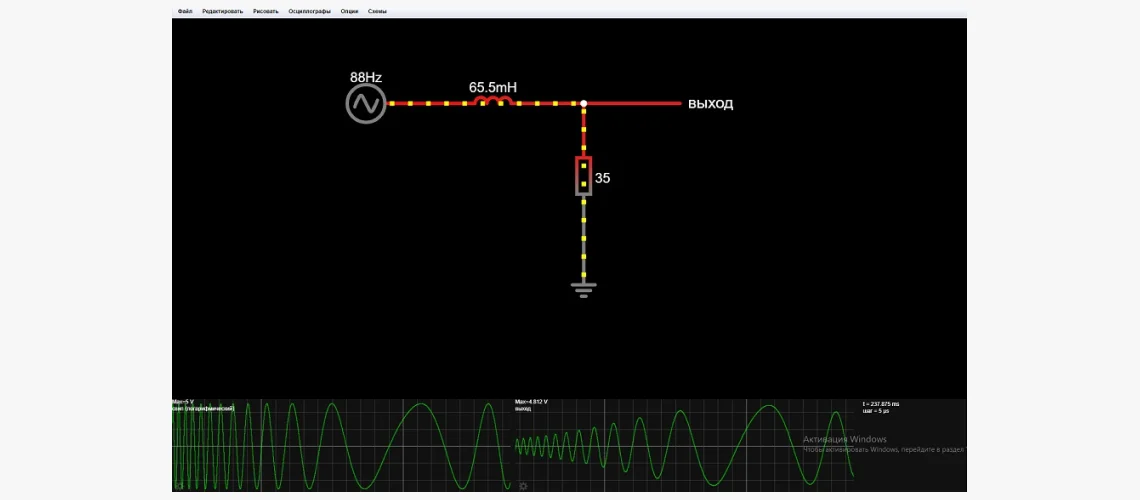
Цепь устройства на рисунке приобретает ПФ:

Это фильтр 2-го порядка. Порядок — наивысшая степень переменной s в ПФ. Он обычно равен общему числу конденсаторов (смотри статью «Как выбрать конденсатор?») и катушек индуктивности в схеме (конденсатор один, даже когда образован последовательным или параллельным соединением двух или больше отдельных; то же относится к катушкам). Варианты более высокого порядка, что очевидно, сложнее и дороже в изготовлении, поскольку они используют больше компонентов, их тяжелее проектировать. Но они эффективнее.
Прежде чем фактически вычислить абсолютное значение ПФ, заметим, что на сверхнизкочастотных уровнях (малые значения s) числитель становится очень маленьким, как и первые два члена знаменателя [4]. Таким образом, когда s приближается к нулю, числитель и H(s) тоже близки к нему, а знаменатель движется к единице.
Аналогично, когда входная частота почти бесконечна, H(s) также становится постепенно меньше, потому как числитель растёт линейно с ней, а знаменатель увеличивается с её квадратом. Следовательно, H(s) будет обладать максимальным значением на некоторой частотности в пределах «нуль–бесконечность» и уменьшаться на уровнях выше и ниже пика.
Чтобы найти значение ПФ амплитуды [5] и фазы [6], заменим s на jω:
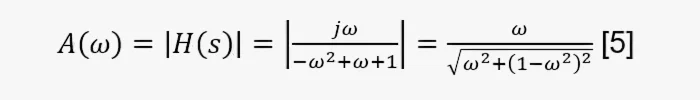
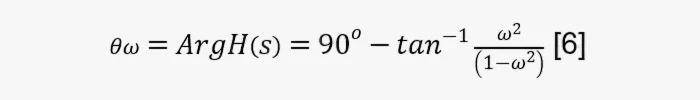
В указанных соотношениях использованы выражения УЧ ω в единицах радиан/секунда. Синусоида совершает один полный цикл за 2π радиан. Когда больше интересует АЧХ и ФЧХ в привычных единицах, таких как герц (Гц, циклов в секунду), преобразуем УЧ, используя выражениеω=2πf, где f — частота в Гц. Переменные f и ω используются более или менее взаимозаменяемо, в зависимости, что уместнее или удобнее для данной ситуации.
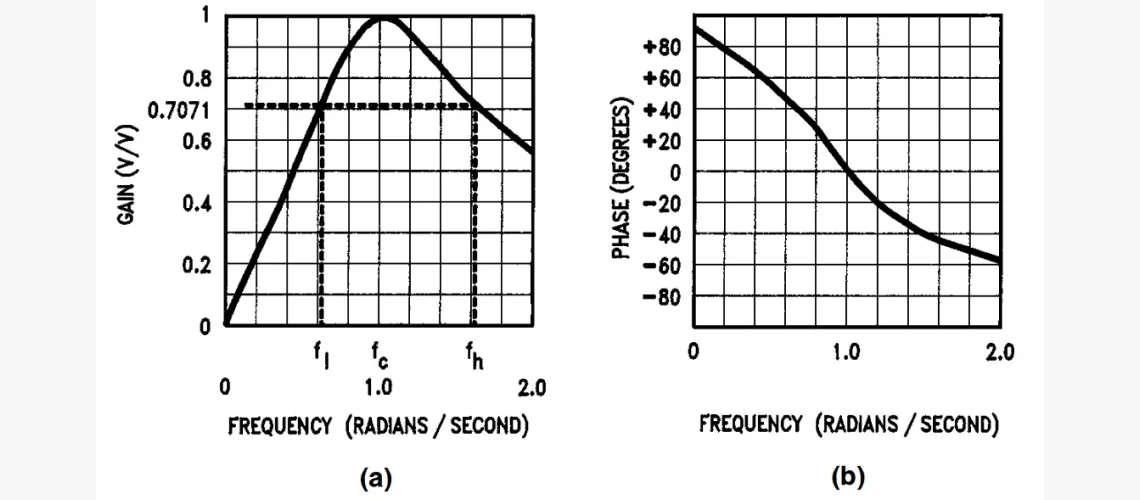
На графике видно, что, как и предсказывали, ПФ показывает максимум значение на определённой частоте (ω0) между 0 и ∞ и спадает по обе стороны. Фильтр с такой общей характеристикой известен как полосовой, потому что пропускает сигналы, попадающие в относительно узкую полосу, и ослабляет за её пределами. Частотный диапазон, пропускаемых им, известен как полоса пропускания (ПП).
Поскольку кривая АЧХ довольно пологая, у ПП нет очевидных границ. Часто её пределы определяются требованиями конкретной области применения компонента. Допустим, системе нужно ослабление в границе 400–1500Гц, не превышающее 1 дБ.
Эта спецификация фактически определяет ПП 400÷1500Гц. В прочих случаях с ПФ работают без обозначенных пределов. Тогда обычно предполагается, что границы ПП являются частотами, на которых происходит ослабление на 3 децибела (до уровня √2/2 или 0.7071 от его максимального усиления по напряжению). Они называются частотами среза (ЧС). Когда явно указано ослабление в ПП-пределах (как в примере, рассмотренном выше, не более 1 дБ), то ЧС станут превышающие максимальное значение ослабление (свыше 1 дБ).
Точная форма АЧХ полосового фильтра (да и любого другого) будет зависеть от конкретной схемотехнической реализации, но при любой ПП характеристика модели 2-го порядка получит пиковое значение на центральной частоте (ЦЧ). Она равна геометрическому среднему ЧС:

где fc — ЦЧ, flow и fhigh — нижняя и верхняя границы ПП соответственно.
Для количественной оценки эффективности используется ещё одна величина — добротность (Q). Это мера «резкости» или «крутизны» амплитудной характеристики. Чем она выше, тем «острее» ПФ-кривая. Параметр Q здесь — это отношение ЦЧ к разнице между ЧС [9]. Таким образом:

При оценке эффективности часто интересует отклик на задаваемом частотном уровне. Таким образом, нужно узнать, какое затухание происходит на двойной ЦЧ и на её половине (ясно, что в случае 2-порядка будет одинаковым в обеих точках). Также необходимо иметь амплитудные и фазовые кривые отклика, охватывающие широкий частотный спектр, а не в пределах ПП-поля. Но достаточно трудно представить их с линейной шкалой, если требуется наблюдать амплитуду и фазу в широком диапазоне.
Например, если f0=1000Гц и требуется оценка отклика на 10000Гц, АЧХ-пик будет близок к левой стороне шкалы. Таким образом, представляет трудность определить амплитуду на, например, 100Гц, так как это значение является 1/100 частью всей шкалы. В подобных случаях полезна логарифмическая шкала, придающая одинаковый вес равным частотным отношениям.
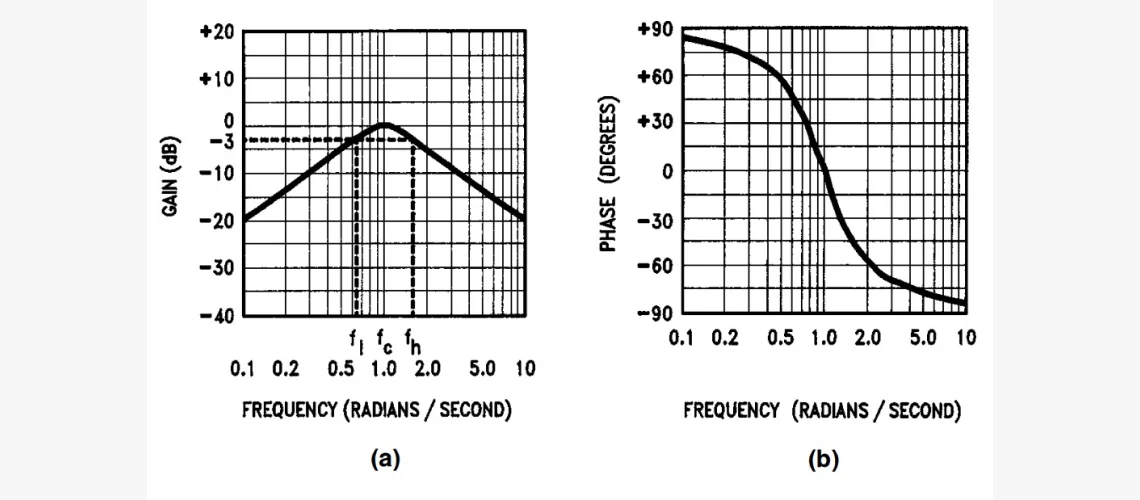
На изображениях заметна возросшая симметрия кривых и повышение общей читабельности.
Основные виды фильтров
Здесь мы рассмотрим распространённые типы устройств фильтрации в электронике. Частично о некоторых разновидностях мы упоминали в статьях «Основы радиочастотной схемотехники. Часть 1, 2, 3». Различные схемотехнические реализации будут рассмотрены позже.
Полосовой фильтр
Он наиболее часто используемым из пятёрки основных разновидностей. Модель, рассмотренная в качестве примера в предыдущем разделе, была именно полосовой. Он предназначен для выделения в ВС-спектре узкочастотной полосы подавления тех, которые не входят в ПП.
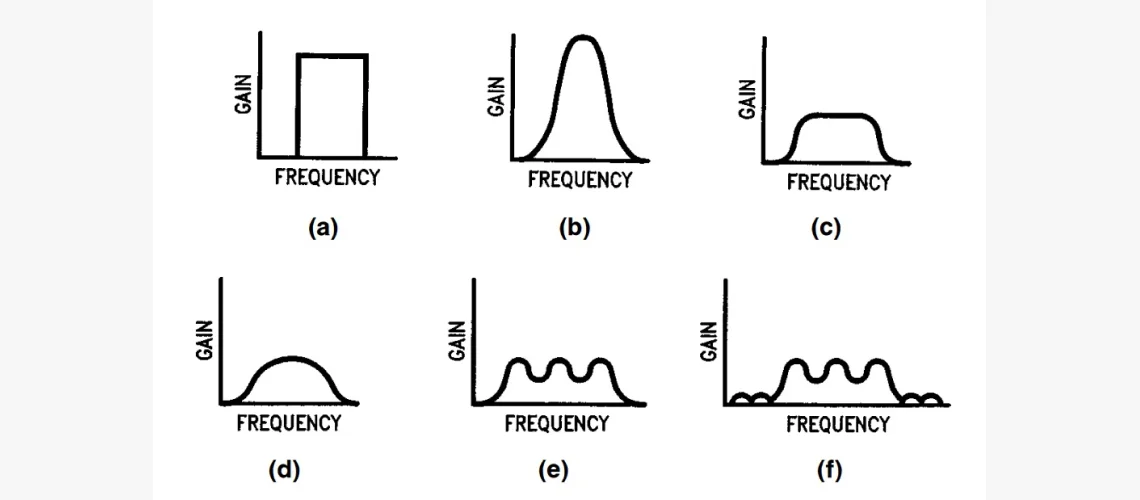
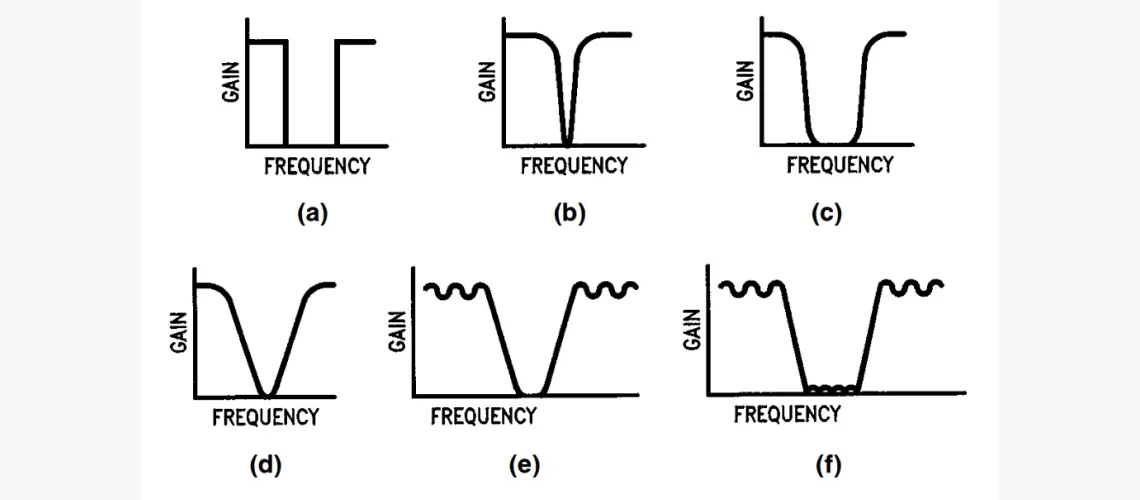
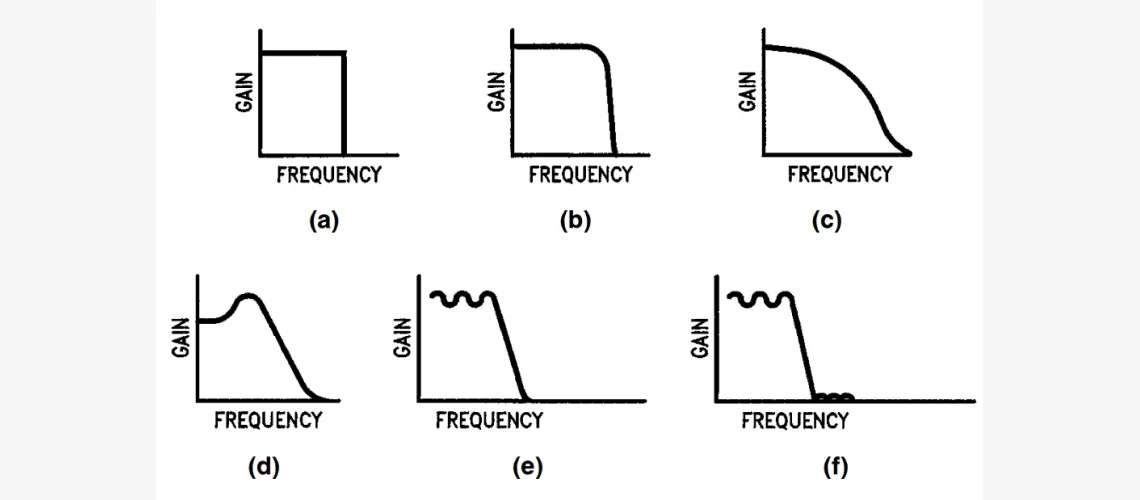
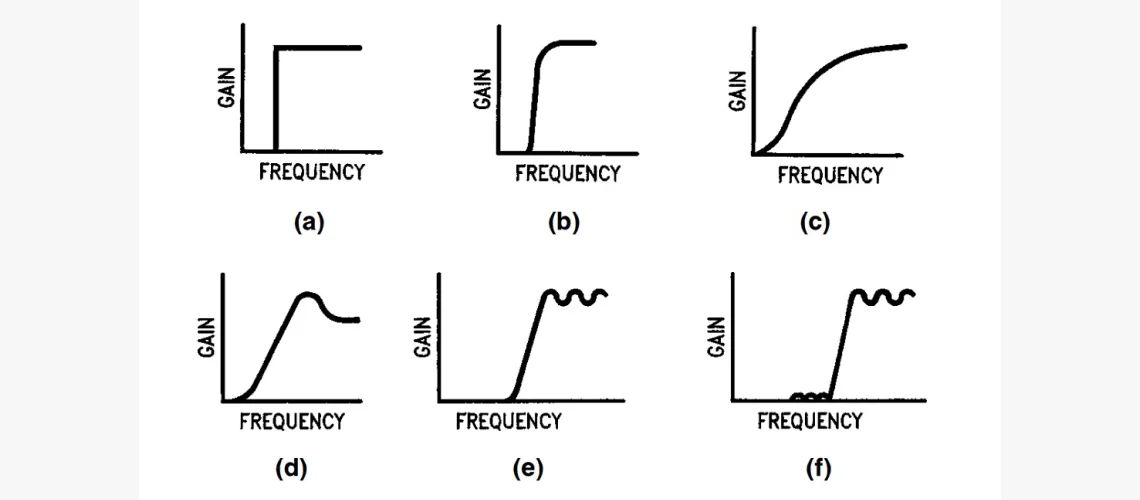
Кривая (a) — это т. н. «идеальная» характеристика отклика с абсолютно постоянным коэффициентом передачи в пределах ПП, нулевым усилением вне её и резкой границей. Её невозможно реализовать на практике, но получается приблизиться с различной степенью точности реальными комплектующими. Кривые (b), (c), (d), (e), (f) являются примерами нескольких АЧХ-кривых, аппроксимирующих идеальную (a) с разной точностью. Хотя часть параметров отклика очень «гладкие» ((b), (c), (d)), у других есть пульсации (изменения усиления в ПП, (e), (f)).
Ещё есть пульсации в полосе задерживания (f). Это диапазон, в котором ослабляются нежелательные частоты ВС. Есть две полосы: выше и ниже ПП.
Насколько сложно определить, что считать за границу ПП, также трудно выявить грани полосы задерживания, редко бывающие чёткими и очевидными. Следовательно, частотность их начала обычно определяется назначением оборудования. Допустим, спецификация потребовала, чтобы сигнал был ослаблен минимум на 35 дБ на 1500Гц. Это предопределило бы начало полосы задерживания на 1500Гц. Скорость изменения затухания (добротность) между полосой пропускания и задерживания тоже отличается в разных фильтрах. Наклон кривой в этой области сильно зависит от порядка, причём варианты высшего порядка имеют более крутые срезы. Он обычно выражается в дБ/октава (октава — это множитель 2 по частоте) или дБ/декада (декада — десятичный).
Используются в электронных системах для отделения сигнала на одной частоте или в пределах частотных полос от разночастотных. Мы рассмотрели пример, где задачей было пропустить нужный сигнал на f1, одновременно максимально ослабляя нежелательный на f2. Эту функцию мог бы выполнять соответствующий радиокомпонент с ЦЧ f1. Он мог бы отклонять «лишние» сигналы на других частотностях за пределами ПП, поэтому полезен в ситуациях, когда интересующий был «загрязнён» сопутствующими ВС на различных уровнях.
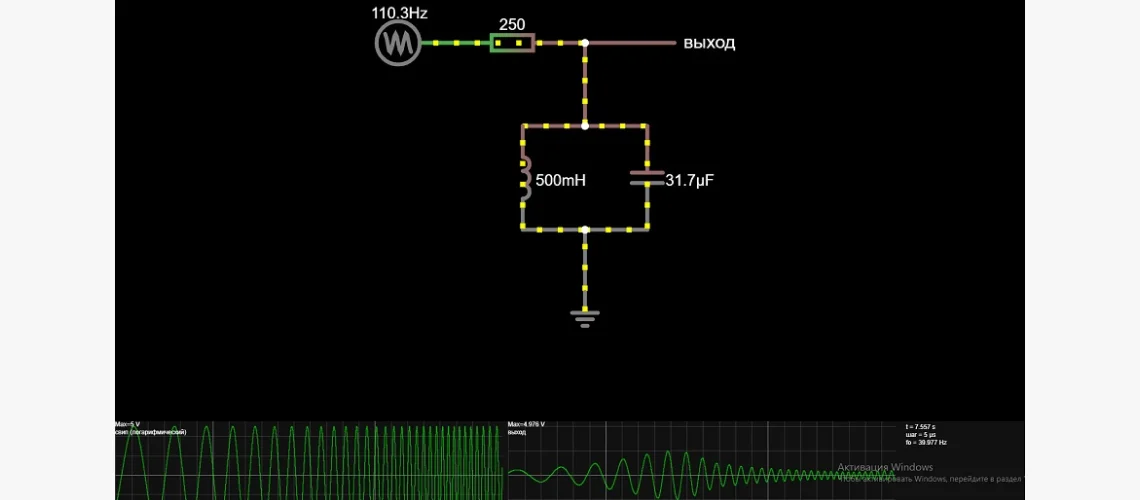
Режекторный фильтр
Он противоположный по функциональным возможностям. Предназначен для подавления определённой частоты или полосы и выделения других частотностей спектра ВС. Если электронные компоненты в цепи фильтра, рассмотренного в предыдущем разделе, переподключить, получим режекторный с ПФ:

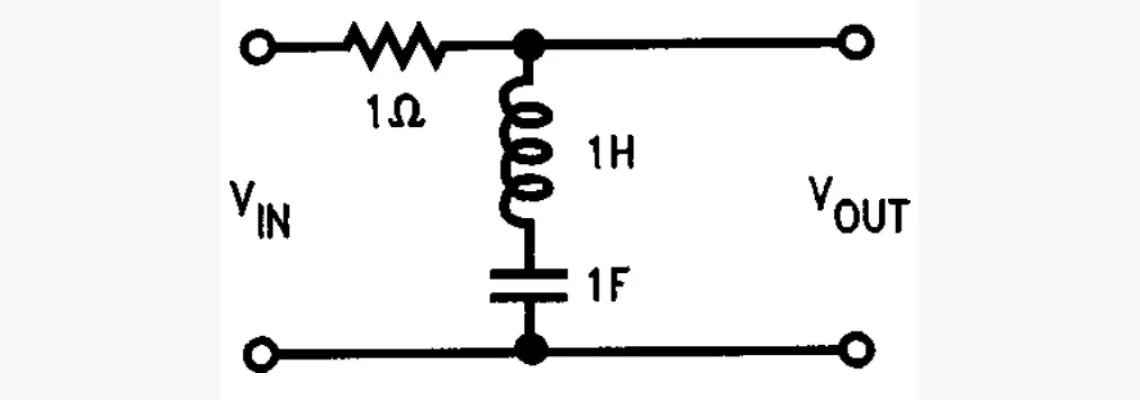
Кривые для схемы отражены на рисунке.
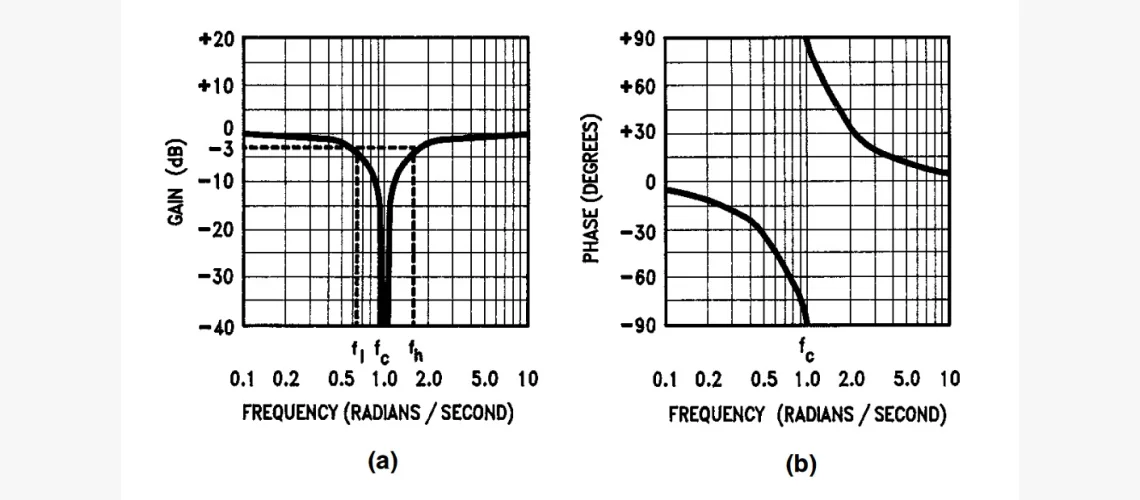
Фильтр нижних частот
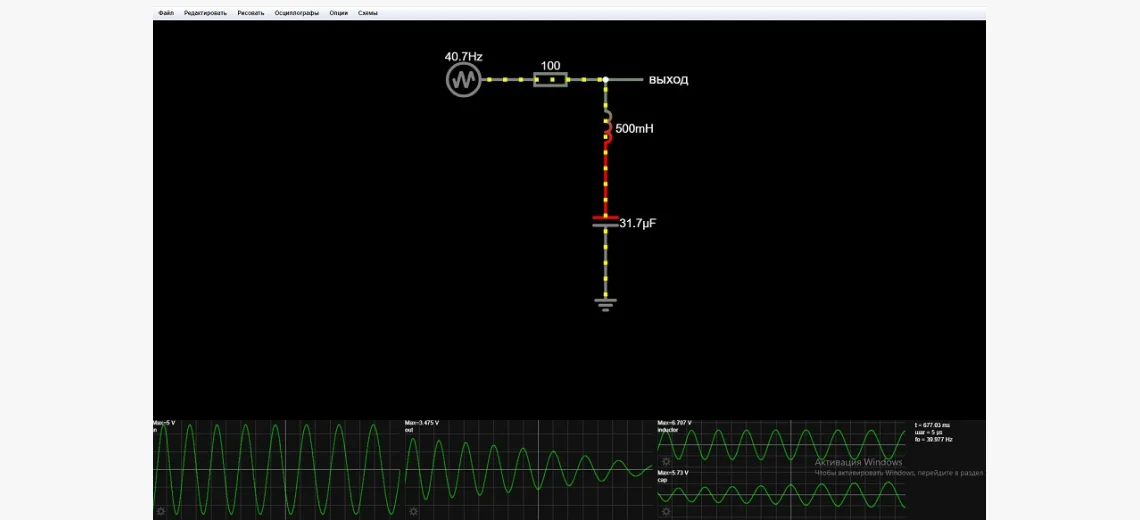
Третий рассматриваемый тип — ФНЧ. Пропускает частоты ниже ЧС и подавляет превышающие. Таким образом, в отличие от полосового и режекторного и аналогично ФВЧ, здесь одна ЧС. Если элементы из первого примера переподключить по схеме ниже, то результирующая ПФ выглядит так:

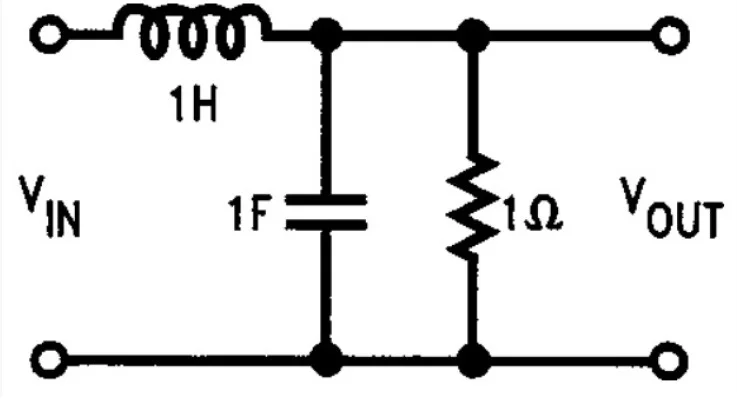
Легко заметить: ПФ имеет большее усиление на низких частотах, чем на высоких. Когда ω приближается к 0, H(s) стремится к 1; а если к бесконечности, то H(s) близится к 0.
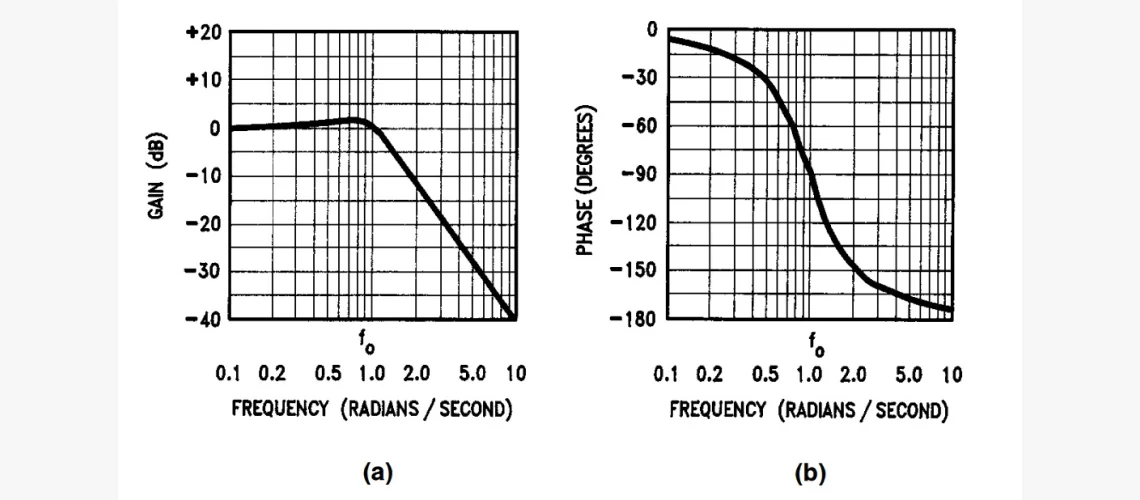
Различные приближения к нереализуемым идеальным АЧХ принимают разные формы, где часть является монотонными (всегда с отрицательным наклоном), а другие имеют пульсацию в полосе пропускания и/или задерживания. ФНЧ используются, когда необходимо удалить высокочастотные компоненты. Примером послужит светочувствительная схема, использующая фотодиод в качестве датчика.
Если уровни освещённости низкие, сигнал на фотодиодном выходе бывает сверхмалым, что позволяет ему быть частично искажённым внутренним шумом датчика и его усилителя, с простирающимся до довольно высокочастотных показателей спектром. Если ФНЧ помещён на выходе усилителя, а его ЧС достаточно высока, чтобы пропустить желаемые частоты, общий уровень шума снижается.
Фильтр верхних частот
Это противоположность ФНЧ. Если электронные компоненты рассматриваемого с начала статьи устройства переподключить по ФВЧ-схеме, то ПФ станет таким:
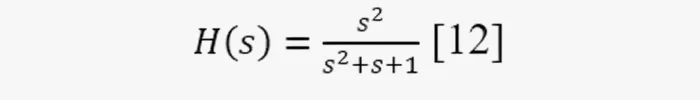
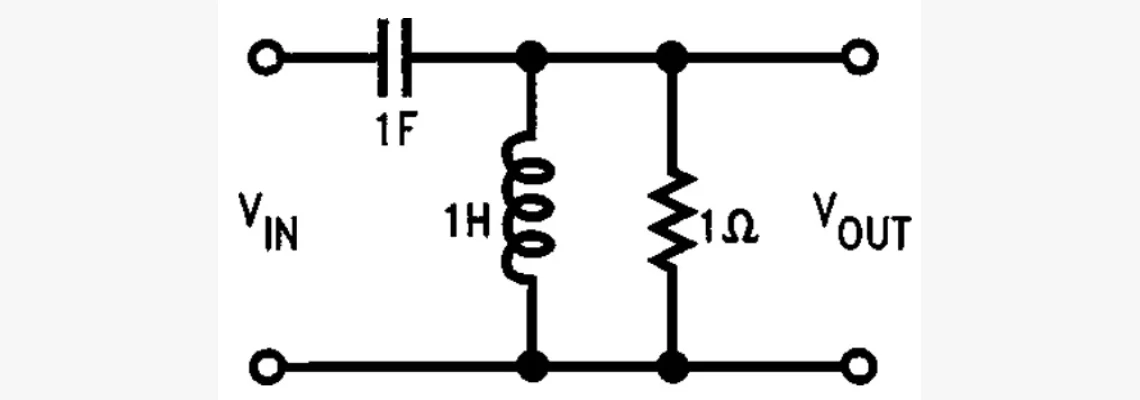
АЧХ у ФВЧ является её «зеркальным отражением» для ФНЧ-устройства. Он используется, где требуется подавление НЧ-сигналов. Например, в HI-end акустических системах. Музыка содержит немало энергии в диапазоне частот от примерно 100Гц до 2кГц, но высокочастотные динамики рискуют повредиться, если на вход подать низкочастотный сигнал. ФВЧ, включённый перед ВЧ-динамиком, не позволит проникнуть НЧ-сигналу.
В сочетании с ФНЧ для НЧ-громкоговорителя (и, возможно, дополнительными фильтрами для прочих динамиков) он является частью кроссовера – специализированного комплексного набора фильтрации для акустических систем.
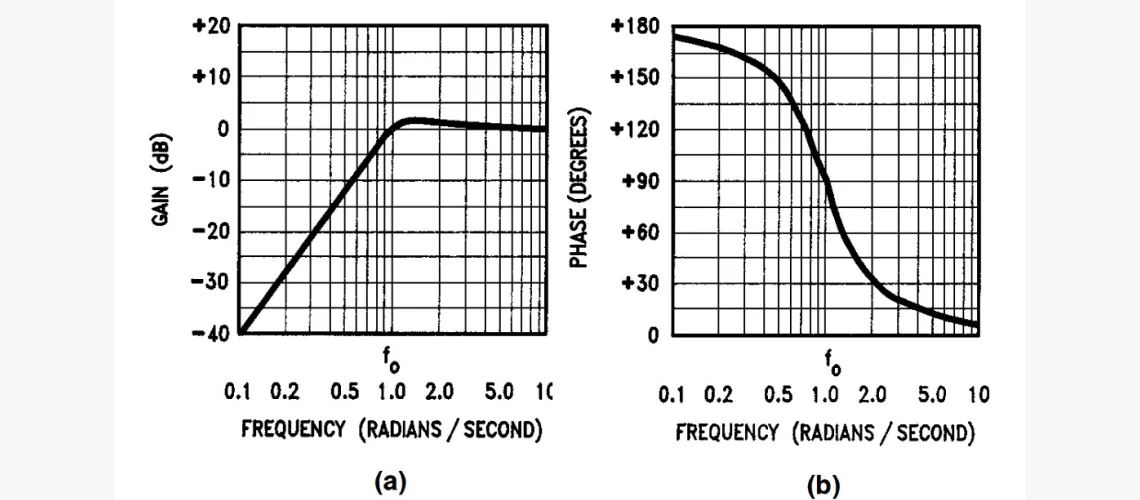
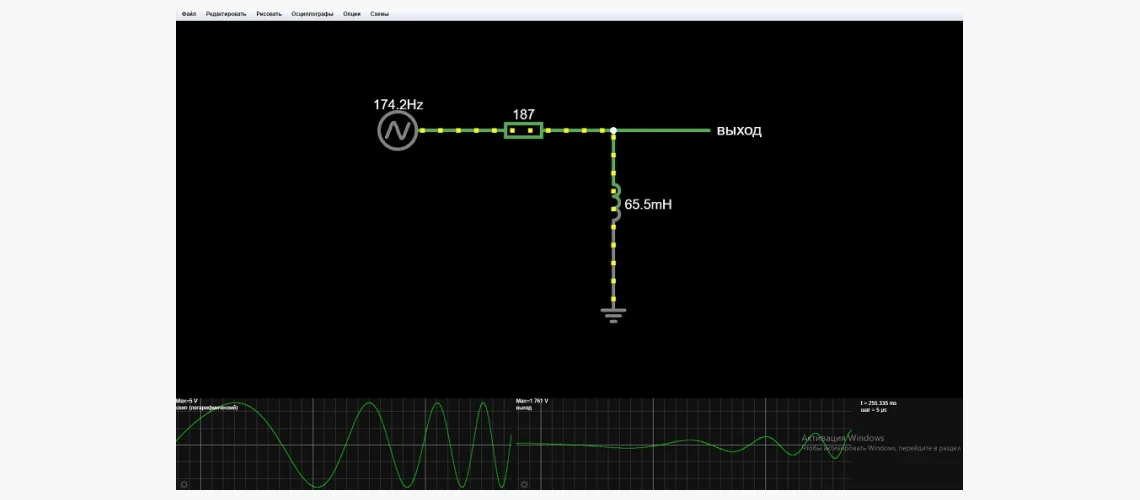
Фазовый фильтр (всечастотный)
В отличие от предыдущих разновидностей, он не влияет на амплитуду сигнала на разных частотах. Вместо этого он меняет фазу. Поэтому часто называется также всечастотным или фильтром с фазовым сдвигом.
Ниже изображены две синусоидальные волны: одна сплошной линией (входной сигнал), а вторая — пунктирной (выходной). Кривые совершенно идентичны, за исключением, что пики и нули пунктирной происходят позже, чем у сплошной. Получается, выходной сигнал претерпел временную задержку относительно входного.
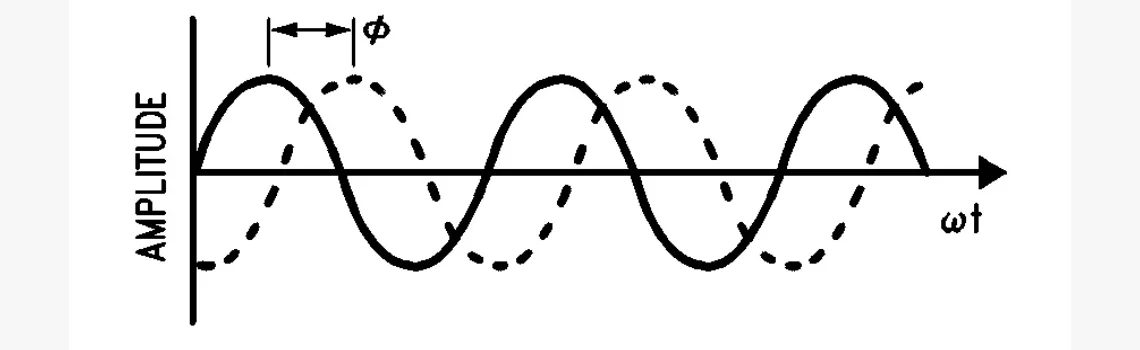
Поскольку работаем с периодическими волнами, время и фаза рассматриваются как взаимозаменяемые параметры: задержка по времени может интерпретироваться как сдвиг фазы пунктирной кривой относительно сплошной. Он здесь равен θ радиан. Его соотношение с задержкой времени равно θ/2 πω, поэтому при постоянстве с частотой временная задержка уменьшается с её ростом.
Такие фильтры обычно используются для введения сдвигов фазы в сигналы для полной или частичной компенсации любых нежелательных сдвигов, приобретённых им, пройдя через другие цепи обработки или средства передачи. Абсолютное значение коэффициента усиления равно единице на всех частотах, но фаза изменяется. На рисунке ниже показана кривая её зависимости от частотности для всечастотного фильтра с ПФ:
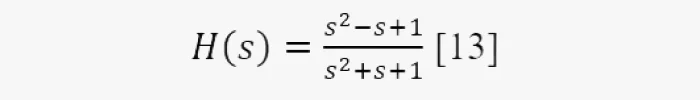
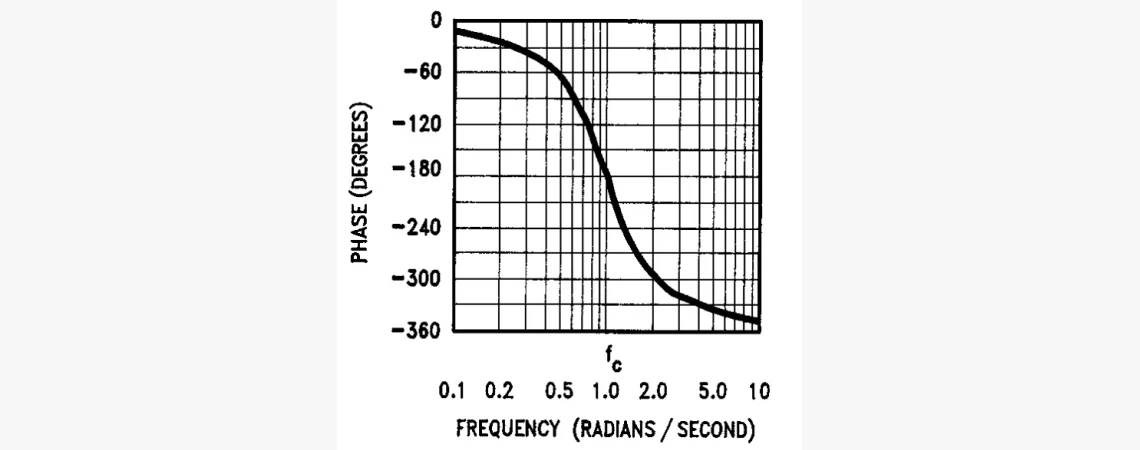
Повторно взглянем на уравнения и кривые. Во-первых, все ПФ имеют один знаменатель. А все числители состоят из членов, найденных в нём: для ФВЧ [12] — первый (s2), для ПФ [4] — второй (s), для ФНЧ [11] — третий (1), а числитель режекторного фильтра [10] — сумма первого и третьего членов знаменателя (s2+ 1). Числитель для ПФ немного отличается тем, что включает все члены знаменателя, но один с отрицательным знаком.
Фильтры второго порядка обладает четырьмя базовыми свойствами:
- разновидностью (полосовой, режекторный и т. д.);
- усилением в ПП (рассмотренные прежде варианты имеют единичное усиление, хотя строятся с любым);
- центральной частотой и добротностью (она определяет относительную форму амплитудной характеристики).
Добротность вычисляется из знаменателя ПФ, если записать в виде:
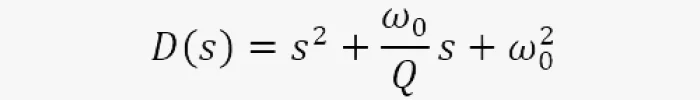
Как уже было отмечено, чем добротность выше, тем «острее» кривая ПФ. ФНЧ и ФВЧ частот имеют острые пики в своих передаточных характеристиках при больших значениях Q.
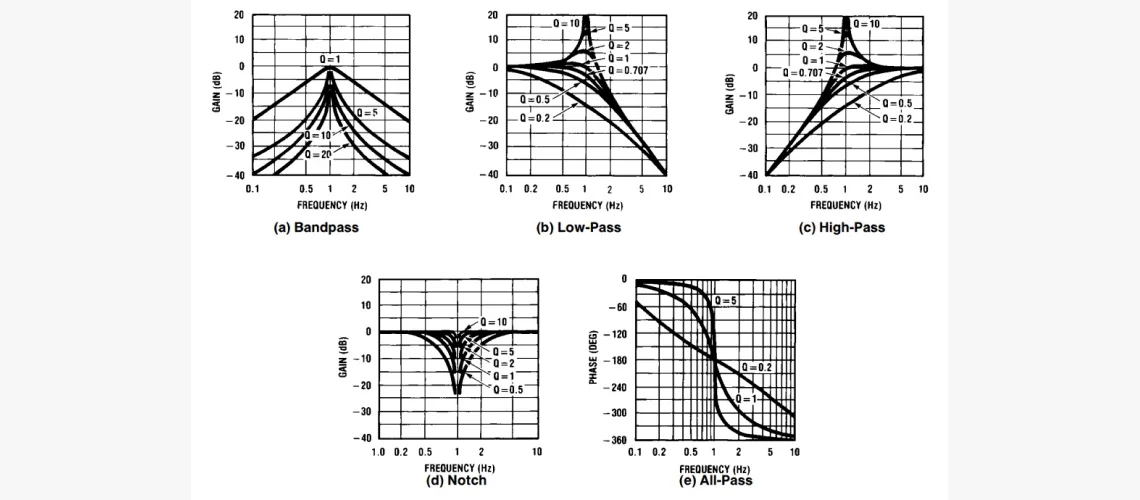
В рассмотренных нами ПФ присутствует симметрия, которая становится очевидной, когда кривые амплитудного отклика построены на логарифмической шкале. У полосового и режекторного фильтров они симметричны относительно f0. Это означает, что их коэффициенты усиления при 2f0 аналогичны, как при f0/2, а при 10f0, — одинаковые с f0/10 и т. д.
Кривые-АЧХ ВЧ- и НЧ-фильтров демонстрируют симметрию. Это зеркальные отражения относительно f0. Таким образом, усиление ФВЧ при 2f0 будет равно ФНЧ-усилению при f0/2 и т. д. Сходства различных функций бывают полезными при создании сложных компонентов. Большинство конструкций начинаются с их определения: к примеру, ФНЧ, разработки протофильтра НЧ, и последующему преобразованию его в полосовой, режекторный или ФВЧ или любой другой требуемый тип после выявления характеристик.
Как видно из кривых для различных типов приборов, их определяемое возможное бесконечно велико. Различия характеристик в пределах одного типа включают, среди прочего, характерные частоты, порядок, наклон спада и плоскостность областей полосы пропускания и задерживания. Передаточная функция, выбранная для конкретной сферы применения, часто будет результатом компромисса указанных параметров.
Читайте продолжение статьи во второй части!
Электроника в целом — безграничная область знаний и занятости человека, которая, как космос, постоянно увеличивается с огромнейшей скоростью. Но разделы науки настолько обширны, что требуют месяцев и лет систематического изучения, чтобы разобраться с базовыми принципами. Одной из областей являются фильтры.
Существует множество решений на разных электронных компонентах, где немало как простых, так и сложнейших формул и методологий для расчёта, а также способов моделирования и проектирования. Они нередко сводят неискушённого (начинающего) радиолюбителя с ума. Но, как говорится, глаза боятся, а руки делают: так вот, начав с основ, доходят и до высших ступеней знаний, позволяющих называться экспертом.








